Answer:
Group 3
Explanation:
The given mean of the population is 55.
For group 1,
Mean = \frac{\sum X}{N}, where X is the all the individual incomes in the group and N is the number of individual incomes in the group.
=
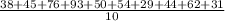
=
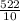
=
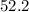
For group 2,
Mean=
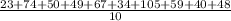
=
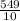
=
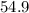
For group 3,
Mean=
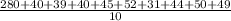
=
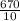
=
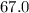
For group 4,
Mean=
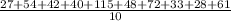
=
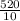
=
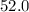
Since, the mean for group 3 is greater than the given mean, therefore group 3 has the largest mean.