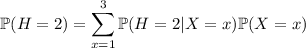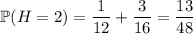I'm assuming this experiment plays out by first rolling the die, and whatever face value occurs determines the number of coin tosses. Let

denote the random variable for the face value of the die. Then the PMF for

is
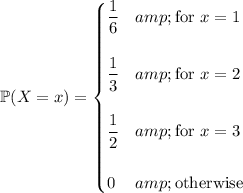
If
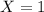
, then only one coin is flipped, so
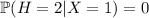
because getting two of any side of the coin is impossible.
If
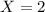
, then the probability of getting two heads is
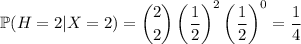
.
If
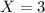
, then the probability of getting two heads is

.
By the law of total probability,