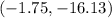We are given the following quadratic equation
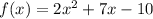
The vertex is the maximum/minimum point of the quadratic equation.
The x-coordinate of the vertex is given by
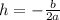
Comparing the given equation with the general form of the quadratic equation, the coefficients are
a = 2
b = 7
c = -10
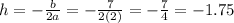
The y-coordinate of the vertex is given by
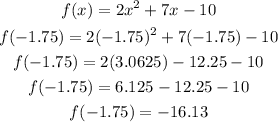
This means that we have a minimum point.
Therefore, the minimum point of the given quadratic equation is