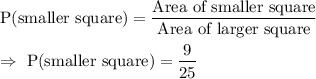Answer:
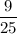
Explanation:
The area of a square is given by :-
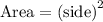
Given: The side length of the smaller square = 3 cm
Then the area of smaller square :-
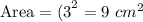
The side length of the larger square = 5 cm
Then the area of larger square :-
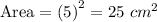
Now, the probability that a point chosen at random in the given figure will be inside the smaller square is given by :-