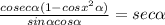Question

Simplify csc θ(1−cos^2 θ)/sinθ cos θ to a single trigonometric function

Answer 1

`(cosec\alpha(1-cosx^(2) \alpha ) )/(sin\alpha cos\alpha ) = sec\alpha`

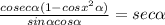
Explanation:

Step(i):-

Given that the trigonometric function

`(cosec\alpha(1-cosx^(2) \alpha ) )/(sin\alpha cos\alpha )`

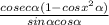
we know that sin²∝ + cos²∝ = 1

⇒ sin²∝ = 1- cos²∝

Now we have to simplify the given trigonometric function

=
`(cosec\alpha(sin^(2) \alpha ) )/(sin\alpha cos\alpha )`

=
`(cosec\alpha(sin \alpha ) )/( cos\alpha )`

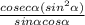
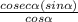
Step(ii)

we know that cosec∝ = 1/ sin∝

=
`((1)/(sin\alpha ) (sin \alpha ) )/( cos\alpha )`

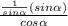
After cancellation sine function, we get

=
`(1 )/( cos\alpha ) = sec\alpha`

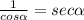
Final answer:-

`(cosec\alpha(1-cosx^(2) \alpha ) )/(sin\alpha cos\alpha ) = sec\alpha`