Question

Suppose that LMN is isosceles with base LN suppose that M

Answer 1

Given:

In an isosceles triangle LMN, LM=MN.

`m\angle M=(3x+17)^\circ,m\angle L=(2x+36)^\circ`

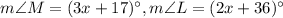
To find:

The measure of the angles L, M and N.

Solution:

In triangle LMN,

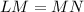`LM=MN` (Given)

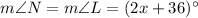`m\angle N=m\angle L=(2x+36)^\circ` (Base angles of an isosceles triangle are equal)

Now,

`m\angle L+m\angle M+m\angle N=180^\circ`

`(2x+36)^\circ+(3x+17)^\circ+(2x+36)^\circ=180^\circ`

`(7x+89)^\circ=180^\circ`

`(7x+89)=180`

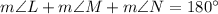
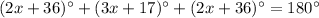
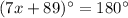
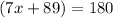
On further simplification, we get

`7x=180-89`

`7x=91`

`x=(91)/(7)`

`x=13`

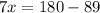
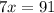
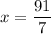
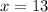
The value of x is 13. Using this value, we get

`m\angle L=(2(13)+36)^\circ`

`m\angle L=(26+36)^\circ`

`m\angle L=62^\circ`

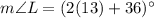
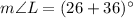
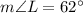
Similarly,

`m\angle M=(3(13)+17)^\circ`

`m\angle M=(39+17)^\circ`

`m\angle M=56^\circ`

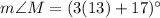
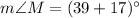
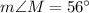
And,

`m\angle N=m\angle L`

`m\angle N=62^\circ`

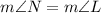
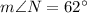
Therefore, the measure of angles are
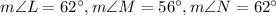`m\angle L=62^\circ,m\angle M=56^\circ,m\angle N=62^\circ`.