Question

A circle has a central angle measuring 90° that intersects an arc of length 117.75 inches.

Using 3.14 for pi, what is the length of the radius of the circle?

_____ inches ?

Answer 1

90 degrees is one quarter of a circle so,
circumference = 4 * 117.75 = 471
circumference = 2 * PI * radius
radius = 471 / (2*PI)
radius = 74.9619781963

Answer 2

Radius = 75 inches .

Explanation:

Given : A circle has a central angle measuring 90° that intersects an arc of length 117.75 inches.

To find : what is the length of the radius of the circle.

Solution : We have given

Central angle = 90°

Arc of length = 117.75 inches.

Arc length =
`(theta)/(360)* 2 \pi * radius`.

Plug the values

Theta = 90 , pi = 3.14 , arc length = 117.75 .

117 .75 =
`(90)/(360)* 2(3.14 ) * radius`.

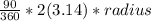117 .75 =
`(1)/(4)* 2(3.14 ) * radius`

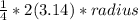
On multiplying both sides 4

117.75 * 4 = 2 * 3.14 * radius .

471 = 6 .28 * radius .

On dividing both sides by 6.28

radius =
`(471)/(6.28)`.

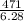Radius = 75 inches .

Therefore, Radius = 75 inches .