Answer:
4 1/2 minutes
Explanation:
This is a classic work problem. These are solved by finding out how much of the work being done can get done in a single unit of time. In our case minutes.
If pipe 1 takes 36 minutes to fill the tank, then it can get 1/36 of the job done in a single minute.
If pipe 2 takes 9 minutes to fill the tank, then it can get 1/9 of the job done in a single minute.
If pipe 3 takes 12 minutes to fill the tank, then it can get 1/12 of the job done in a single minute.
The sum of all of these together will take x minutes. Our equation then is this:

We need to find the LCD of those numbers and multiply through by that LCD to get rid of the fractions, cuz who likes fractions?! The LCD is 36x; each denominator, including the x, goes into 36x evenly and that's the lowest number that each goes into evenly. Multiplying through by the LCD:
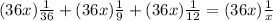
Reducing gives us the equation:
x + 4x + 3x = 36 and
8x = 36 so
x = 4.5 minutes or 4 1/2 minutes