Answer:
Option 4 is correct that is
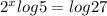
Explanation:
We have been given the expression:
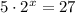
Since, Gabriel used logarithms to solve the given equation
Taking log on both sides of the equation we get:
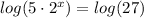
We will use the property of logarithmic function which is :

Here, on left hand side of the equation
 we get:
we get:
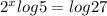
Hence, option 4 is correct.