Question

Suppose the population of a town is 100,000 in 1999. The population increases at a rate of 4.5% every year. What will be the population of the town in 2005? Round your answer to the nearest whole number.

Answer 1

100,000 * (1.045)^years
2005 Population = 100,000 * (1.045)^6
= 100,000 * 1.3022601248
= 130,226

Answer 2

130,226.

Explanation:

We have been given that the population of a town is 100,000 in 1999. The population increases at a rate of 4.5% every year.

We will use exponential growth function to solve our given problem. We know that exponential function is in form
`f(x)=a\cdot b^x`, where,

`f(x)` = Final value,

a = Initial value,

b = For growth b is in form
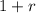`1+r`, where r represents rate in decimal form.

Let us convert 4.5% into decimal form.

`4.5\%=(4.5)/(100)=0.04`

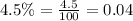
Upon substituting our given values in exponential growth formula, we will get:

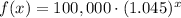`f(x)=100,000\cdot (1.045)^x`, where x represents number of years after 1999.

To find population of town in 2005, we will substitute
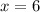`x=6` (2005-1999=6) in our function.

`f(6)=100,000\cdot (1.045)^6`

`f(6)=100,000\cdot 1.3022601248475156`

`f(6)=130,226.01248475156`

`f(6)\approx 130,226`

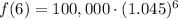
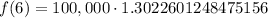
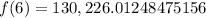
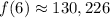
Therefore, the population of the town in 2005 will be 130,226.