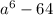Question

Find the product. (a3 + 8)(a3 – 8)

A.) a6 – 16n3 + 64

B.) a6 – 16n3 – 64

C.) a6 – 512

D.) a6 – 64

Answer 1

1. Use difference of squares: a^2-b^2=(a+b)(a-b)
(a^3)^2-8^2
2. Use power rule: (x^a)^b=x^(ab)
a^6-8^2
3. Simplify 8^2 to 64
a^6-64

Your answer is d.

Answer 2

Option: D is the correct answer.

The product is:

D.
`a^6-64`

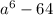
Explanation:

We are asked to simplify the given algebraic expression i.e. we have to find the product of two algebraic expressions, which are a polynomial in terms of "a"

As both are cubic polynomial so there product will be a six-degree polynomial.

( Since on multiplying the degree gets add up )

The expression is as follows:

`(a^3+8)(a^3-8)`

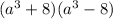
We know that:

`(a+b)(a-b)=a^2-b^2`

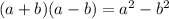
Hence we get the product as:

`(a^3+8)(a^3-8)=(a^3)^2-(8)^2\\\\\\i.e.\\\\\\(a^3+8)(a^3-8)=a^6-64`

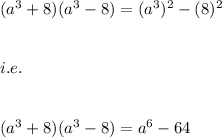
Hence, the product is:

`a^6-64`