Question

The speed of a moving bullet can be deter-

mined by allowing the bullet to pass through
two rotating paper disks mounted a distance
61 cm apart on the same axle. From the
angular displacement 14° of the two bullet
holes in the disks and the rotational speed
1436 rev/min of the disks, we can determine
the speed of the bullet.

Answer 1

v = 381 m/s

Step-by-step explanation:

Linear Speed

The linear speed of the bullet is calculated by the formula:

`\displaystyle v=(x)/(t)`

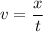
Where:

x = Distance traveled

t = Time needed to travel x

We are given the distance the bullet travels x=61 cm = 0.61 m. We need to determine the time the bullet took to make the holes between the two disks.

The formula for the angular speed of a rotating object is:

`\displaystyle \omega=(\theta)/(t)`

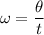
Where θ is the angular displacement and t is the time. Solving for t:

`\displaystyle t=(\theta)/(\omega)`

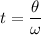
The angular displacement is θ=14°. Converting to radians:

`\theta=14*\pi/180=0.2443\ rad`

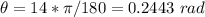
The angular speed is w=1436 rev/min. Converting to rad/s:

`\omega = 1436*2\pi/60=150.3776\ rad/s`

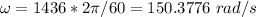
Thus the time is:

`\displaystyle t=(0.2443\ rad)/(150.3776\ rad/s)`

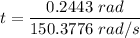
t = 0.0016 s

Thus the speed of the bullet is:

`\displaystyle v=(0.61)/(0.0016)`

v = 381 m/s