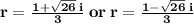Question

1) 3r² – 2r=-9
Quadratic formula

Answer 1

Solving the equation
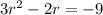`3r^2-2r=-9` using quadratic formula we get:
`\mathbf{ r=(1+√(26)\:i)/(3)\:or\: r=(1-√(26)\:i)/(3)}`

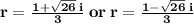
Explanation:

We need to solve the equation
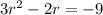`3r^2-2r=-9` using quadratic formula.

The quadratic formula is:
`r=(-b\pm√(b^2-4ac))/(2a)`

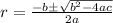
For the given equation:
`3r^2-2r=-9`

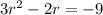
We can write it as:
`3r^2-2r+9=0`

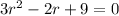
We have a = 3, b= -2 and c=9

Putting values in quadratic formula and finding value of r

`r=(-b\pm√(b^2-4ac))/(2a)\\r=(-(-2)\pm√((-2)^2-4(3)(9)))/(2(3))\\r=(2\pm√(4-108))/(6)\\r=(2\pm√(-104))/(6)\\We\:know\:that: √(-1)=i\\ r=(2\pm√(26) \:i)/(6)\\ r=(2+2√(26)\:i)/(6)\:or\: r=(2-2√(26)\:i)/(6)\\ r=(2(1+√(26)\:i))/(6)\:or\: r=(2(1-√(26)\:i))/(6)\\ r=(1+√(26)\:i)/(3)\:or\: r=(1-√(26)\:i)/(3)`

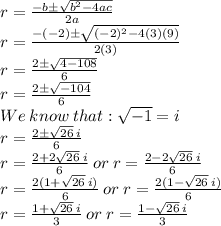
So, solving the equation
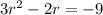`3r^2-2r=-9` using quadratic formula we get:
`\mathbf{ r=(1+√(26)\:i)/(3)\:or\: r=(1-√(26)\:i)/(3)}`