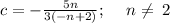Question

4/2n+5/3c=1
Solve for c.

-Multiply both sides by (blank) to clear fractions.

Answer 1

We conclude that:

`c=-(5n)/(3\left(-n+2\right));\quad \:n\\e \:2`

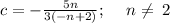
Explanation:

Given the expression

`(4)/(2n)+(5)/(3c)=1`

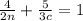
Let us solve for 'c'

`(4)/(2n)+(5)/(3c)=1`

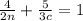
Least Common Multiplier of 2n, 3c: 6nc

Now multiply both sides by LCM = 6nc

`(4)/(2n)\cdot \:6nc+(5)/(3c)\cdot \:6nc=1\cdot \:6nc`

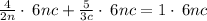
Simplify

`12c+10n=6nc`

Subtract 10n from both sides

`12c+10n-10n=6nc-10n`

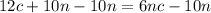
Simplify

`12c=6nc-10n`

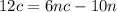
Subtract 6nc from both sides

`12c-6nc=6nc-10n-6nc`

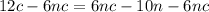
Simplify

`12c-6nc=-10n`

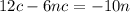
Factor 12c - 6nc = 6c(2-n)

`6c\left(2-n\right)=-10n`

Divide both sides by 6(2-n); n≠2

`(6c\left(2-n\right))/(6\left(2-n\right))=(-10n)/(6\left(2-n\right));\quad \:n\\e \:2`

simplify

`c=-(5n)/(3\left(-n+2\right));\quad \:n\\e \:2`

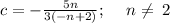
Therefore, we conclude that:

`c=-(5n)/(3\left(-n+2\right));\quad \:n\\e \:2`