Question

Consider the arithmetic sequence:

10, 12, 14, 16, ...
If n is an integer, which of these functions generate the sequence?
Choose all answers that apply:
a(n) = 16 + 3n for n 2-2
A
b(n) = 14 + 2n for n > -1
c(n) = 10 + 3n for n > 0
Dd(n) = 8 + 2n for n > 1

Answer 1

D) 8 + 2n for n > 1

Explanation:

Answer 2

If n is an integer, the function that generate the sequence 10, 12, 14, 16, ... is
`\mathbf{d(n)=8+2n\:for\:n>1}`

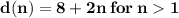
Option D is correct option

Explanation:

We are given the arithmetic sequence:

10, 12, 14, 16, ...

If n is an integer, which of these functions generate the sequence?

We need to find the nth term for the given sequence

The nth term for arithmetic sequence will be:
`a_n=a_1+(n-1)d`

where aₙ is nth term, a₁ is first term and d is common difference

Looking at the sequence a₁ = 10 and d = 2

So, nth term will be:

`a_n=a_1+(n-1)d\\a_n=10+(n-1)2\\a_n=10+2n-2\\a_n=8+2n`

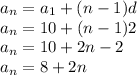
So, nth term is:
`a_n=8+2n`

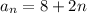
In the options below, the only correct answer is option D. so, we can write nth term as:
`d(n) = 8 + 2n\: for\: n > 1`

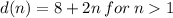
So, If n is an integer, the function that generate the sequence 10, 12, 14, 16, ... is
`\mathbf{d(n)=8+2n\:for\:n>1}`

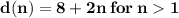
Option D is correct option