Let x be the number of couple tickets and let y be the number of single tickets sold.
We know that the school earned a total of $7050, then we have that:
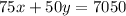
Now, we also know that the total number of students was 173, then we have:
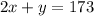
Hence we have the system of equations:
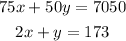
To solve this system we multiply the second equation by -50, then we have:
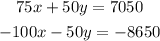
Adding this equation we have:
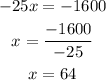
Once we know the value of x we plug it in the second equation to get y:
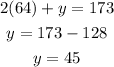
Therefore, they sold 64 couple tickets and 45 single tickets.