Question

C is the center of the circle.

In order to prove that opposite angles of a quadrilateral inscribed in a circle are supplementary (in this case m∠EDG + m∠EFG = 180°), which fact is MOST important to know?

Answer 1

I hope this helps you

Answer 2

Option D is correct.

Explanation:

Given C is the center of the circle.

we have to prove opposite angles of a quadrilateral inscribed in a circle are supplementary.

By the theorem, the angle subtended by an arc at the center is double the angle subtended at any point on the circumference of a circle.

i.e
`\angle ECG=2\angle EDG\\\\\angle EDG=(1)/(2)\angle ECG\thinspace \thinspace \thinspace i.e \thinspace \thinspace \thinspace \angle EDG=(1)/(2)\angle1\\\\\angle EFG=(1)/(2)\angle ECG\thinspace \thinspace \thinspace i.e \thinspace \thinspace \thinspace \angle EFG=(1)/(2)\angle2\\\\As, \angle1+\angle2=360^(\circ)\\\\\angle EDG + \angle EFG=(1)/(2)\angle1+(1)/(2)\angle2=(1)/(2)(\angle1+\angle2)=(1)/(2)* 360=180^(\circ)`

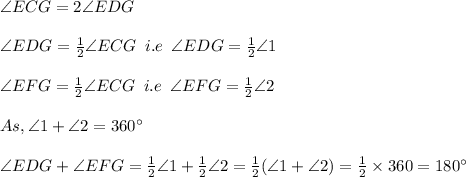
Hence, the fact which is used to prove the above is

`\angle EDG=(1)/(2)\angle ECG`

i.e option D is used.