Answer:
Explanation:
Given: Kite QRST has a short diagonal of QS and a long diagonal of RT. The diagonals intersect at point P. Side QR = 5m and diagonal QS = 6m.
Since, diagonals of kite bisect each other, thus QP=6m
Now, in ΔPQR, we have
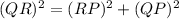
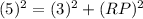
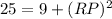
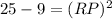
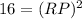

Therefore, the length of segment RP is 4m.