Question

Find the standard form of the equation of the parabola with a focus at (3, 0) and a directrix at x = -3.

a) y = (1/12)x^2
b) -12y = x^2
c) x = (1/12)y^2
d) y^2 = 6x

Answer 1

notice the picture below

the directrix is a vertical line, and the focus point is to the right of it
the vertex is always half-way between those two, at h,k coordinates

thus the parabola is opening sideways, to the right, thus the "y" is the
variable that's at the second power

or
`\bf \begin{array}{llll} \boxed{(y-{{ k}})^2=4{{ p}}(x-{{ h}})} \\\\ (x-{{ h}})^2=4{{ p}}(y-{{ k}})\\ \end{array} \qquad \begin{array}{llll} vertex\ ({{ h}},{{ k}})\\ {{ p}}=\textit{distance from vertex to }\\ \qquad \textit{ focus or directrix} \end{array}`

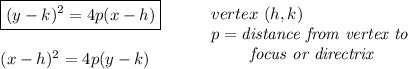
so... use those values, and plug them in the equation