Question

Y2-3y1+2y=e^x/1+e^x,, solution by varation of paramaters(Wronskiam)

Answer 1

To solve via variation of parameters, you first need two linearly independent solutions. You can find them by solving the homogeneous part.


`y''-3y'+2y=0`

has characteristic equation


`r^2-3r+2=(r-2)(r-1)=0`

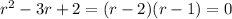
which has roots
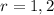
`r=1,2`. So the characteristic solution is


`y_c=C_1e^x+C_2e^(2x)`

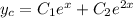
with two linearly independent solutions,
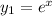
`y_1=e^x` and
`y_2=e^(2x)`.

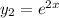
Now when using variation of parameters, you're looking for solutions
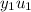
`y_1u_1` and
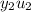
`y_2u_2` where


`u_1=-\displaystyle\int(y_2(e^x)/(1+e^x))/(W(y_1,y_2))\,\mathrm dx`

`u_2=\displaystyle\int(y_1(e^x)/(1+e^x))/(W(y_1,y_2))\,\mathrm dx`

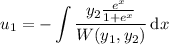
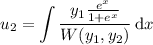
with
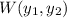
`W(y_1,y_2)` denoting the Wronskian of the characteristic solutions.

You have


`W(y_1,y_2)=\begin{vmatrix}e^x&e^(2x)\\e^x&2e^(2x)\end{vmatrix}=2e^(3x)-e^(3x)=e^(3x)`

`u_1=-\displaystyle\int(e^(-x))/(1+e^x)\,\mathrm dx=-x+\ln(1+e^x)`

`u_2=\displaystyle\int\frac1{1+e^x}\,\mathrm dx=-e^(-x)+\ln(1+e^(-x))`

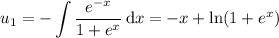
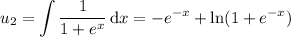
and so the particular solution is


`y_p=y_1u_1+y_2u_2`

`y_p=-xe^x+e^x\ln(1+e^x)-e^x+e^(2x)\ln(1+e^(-x))`

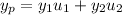
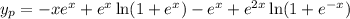
The general solution is then


`y=y_c+y_p`

`y=C_1e^x+C_2e^(2x)-xe^x+e^x\ln(1+e^x)+e^(2x)\ln(1+e^(-x))`

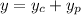
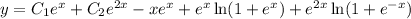
where the
`e^x` term from
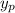
`y_p` gets absorbed into the same term from
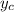
`y_c`.