Question

A car accelerates uniformly from rest and

reaches a speed of 9.2 m/s in 9.7 s. The
diameter of a tire is 47.8 cm.
Find the number of revolutions the tire
makes during this motion, assuming no slip-
ping
Answer in units of rev.

Answer 1

29.75 revolutions

Step-by-step explanation:

The kinematic formula for distance, given a uniform acceleration a and an initial velocity v₀, is

`d=v_0t+(1)/(2)at^2`

This car is starting from rest, so v₀ = 0 m/s. Additionally, we have a = 9.2/9.7 m/s² and t = 9.7 s. Plugging these values into our equation:

`d=0t+(1)/(2)\left((9.2)/(9.7)\right)(9.7)^2\\d=(1)/(2)(9.2)(9.7)\\d=4.6(9.7)\\d=44.62`

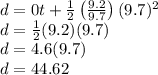
So, the car has travelled 44.62 m in 9.7 seconds - we want to know how many of the tire's circumferences fit into that distance, so we'll first have to calculate that circumference. The formula for the circumference of a circle given its diameter is
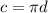`c=\pi{d}`, which in this case is 47.8π cm, or, using π ≈ 3.14, 47.8(3.14) = 150.092 cm.

Before we divide the distance travelled by the circumference, we need to make sure we're using the same units. 1 m = 100 cm, so 105.092 cm ≈ 1.5 m. Dividing 44.62 m by this value, we find the number of revs is

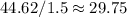`44.62/1.5\approx29.75` revolutions