Question

The function f(x) = 4(3)x represents the growth of a dragonfly population every year in a remote swamp. Erin wants to manipulate the formula to an equivalent form that calculates four times a year, not just once a year. Which function is correct for Erin's purpose, and what is the new growth rate?

Answer 1

F(x)=4(3^(1/4))^4x ....131.6%

Answer 2

`f(x)=4(1.32)^(4x)`

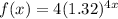
New growth rate = 32%

Explanation:

∵ The exponential growth function is,

`f(x)=a(1+b)^x`

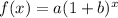
Where,

a = initial value,

b = growth rate per period,

x = number of period,

Here, the given function that shows the population growth every year,

`f(x)=4(3)^x=4(1+2)^x`

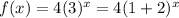
By comparing,

Initial population, a = 4,

Let r be the rate per 4 times a year,

Thus, the function that shows the population growth four times a year,

`f(x)=4(1+r)^(4x)`

According to the question,

`4(1+r)^(4x)=4(3)^x`

`(1+r)^x=3^x`

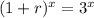
Taking log both sides,

`x\log(1+r)=x\log3`

`\log(1+r)=\log3`

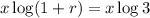
By graphing calculator,

`r=0.316=31.6\% \approx 32\%`

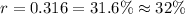
Hence, the required function would be,

`f(x)=4(1+0.32)^x=4(1.32)^x`

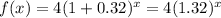
And, rate per period is 32%.