A. We have a normally distribute random variable with mean of 2.9 years and standard deviation of 0.9 years.
We have to find the probability that a random selected individual of this population will last longer than 5 years.
To find this we calculate the z-score for X = 5 and then calculate the probability.
We can calculate the z-score as:
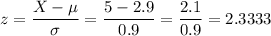
We can now use this z-score and calculate the probability from the standard normal distribution:
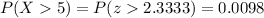
Answer: the probability that a random selected item last longer than 5 years is 0.0098.
B. In this case, the random variable is normal and has a mean of 450 g and a standard deviation of 35 g,
We have to find the the probability that the random selected fruit will weigh between 352 grams and 470 grams.
We now calculate the z-score for both limits of the interval:
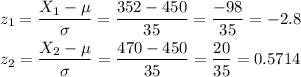
Now, we can calculate the probability that is within this interval as:
![\begin{gathered} P\mleft(352<strong>Answer: The probability that it will weigh between 352 grams and 470 grams is 0.7136.</strong><p></p><p>C) In this case, the distribution has a mean of 560 g and a standard deviation of 13 g,</p><p></p><p>We have to find the weight for which only 9% of the fruits are above that weight.</p><p>In this case, we have to work backwards: we start with the standard normal ditribution.</p><p></p><p>From table (or an app or calculator), we know that:</p>[tex]P(z>1.34076)=0.09]()
Then, knowing the z-score for which only 9% of the data is greater than it, we can convert it to our distribution:
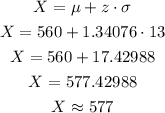
Answer: Approximately 9% of the fruit will weight more than 577 grams.
D. We have this random normal variable (daily production of milk per cow) with mean of 33 L and standard deviation of 2.8 L.
We have to find the probability that the production is less than 34.7 L.
We start by calculating the z-score:
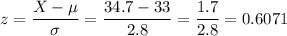
Then, we use an app or calculator to calculate the probability:
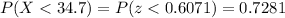
To calculate the probability that the production is more than 28.3 L, we have to proceed similarly:
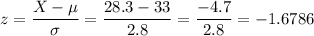
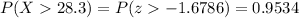
Answer:
The probability that the production is less than 34.7 L is 0.7281.
The probability that the production is more than 28.3 L is 0.9534.