Question

A circle has a radius of 6 in. The circumscribed equilateral triangle will have an area of:

Answer 1

The area of the equilateral triangle is 216 sq. inches.

Explanation:

Given : A circle has a radius of 6 in.

To find : The circumscribed equilateral triangle will have an area of?

Solution :

We draw a rough sketch of the given situation,

Form an equilateral triangle PQR in which a circle in circumscribed with radius r and center O.

Refer the attached figure below.

Radius of the circle is 6 inches.

In ΔPQR,

Top find the area of the equilateral triangle we need to find the length of the base(b) i.e. QR and it's height(h) i.e. PT.

Area of the triangle is
`A=(1)/(2)* b* h`

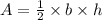
Now we apply the trigonometric identity in ΔOTR.

Since, QR=2 TR

In ΔOTR,

`\sin 30=(OT)/(TR)\\\\(1)/(2)=(6)/(TR)\\\\TR=12`

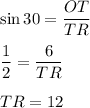
QR=2 TR=2(12)=24 in is base of the triangle.

Now in ΔPOS,

`\cos 60=(OS)/(PO)\\\\(1)/(2)=(6)/(PO)\\\\PO=12 in.`

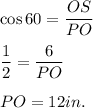
AD=AO+OD

AD=12+6=18 in. is the height of the triangle.

Hence,

Area of the triangle is

`A=(1)/(2)* b* h`

`A=(1)/(2)* 18* 24`

`A=216`

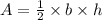
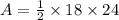
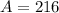
Therefore, The area of the equilateral triangle is 216 sq. inches.

Answer 2

the length of the side of an equilateral triangle that is circumscribed by a circle with radius r is s = r sqrt(3)
so s = (6) sqrt(3)
then the formula for the area of an equilateral triangle is
A = sqrt(3) (s^2) / 4

substitute the value of s in the equation
A = sqrt(3) ( (6) sqrt(3))^2 /4
A = 46.77 sq in