Answer:
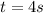
Explanation:
The vertical displacement of an object in freefall is given by the next equation:
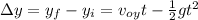
Where:

This equation can be reduced to the equation given by the problem since:
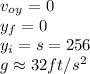
Hence:
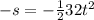
Solving for t:
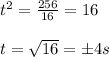
Since a negative time wouldn't have sense, the answer is 4 seconds