Question

A set of test scores is normally distributed with a mean of 145 and a standard deviation of 11. Seif received a score of 167. What was his percentile score

97.5%

84%

95%

63.5%

Answer 1

Since
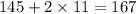
`145+2*11=167`, which means the corresponding z-score for Seif's test score is
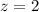
`z=2`. The empirical rule asserts that for any normal distribution, approximately 95% of it lies within two standard deviations of the mean, i.e.
`\mathbb P(|Z|<2)=0.95`, which leaves 5% outside of that range, and specifically 2.5% to either side.

This means


`\mathbb P(Z<2)=\mathbb P(Z<-2)+\mathbb P(|Z|<2)=0.025+0.95=0.975`

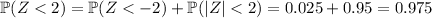
In other words, a test score of 167, which corresponds to a z-score of 2, marks the 97.5th percentile.