Question

A cone with volume 1350 m³ is dilated by a scale factor of 13.

What is the volume of the resulting cone?

Answer 1

50 m³

(1/3)³ = (0.037037037)*(1350) = 50

Answer 2

Answer: The answer is 2965950 m³.

Step-by-step explanation: Given that the volume of a cone is 1350 m³. We need to find the volume of the resulting cone when the original cone is dilated by a scale factor of 13.

We know that the volume of a cone with radius of the base 'r' and height 'h' is given by

`V_o=(1)/(3)\pi r^2h=1350~\textup{m}^3.`

After dilation, both the radius and height will be increased by 13 times, so the new volume of the resulting cone will be

`V_r=(1)/(3)\pi(13r)^2(13h)\\\\\Rightarrow V_r=13^3* (1)/(3)\pi r^2h\\\\\Rightarrow V_r=13^3* V_o\\\\\Rightarrow V_r=2197* 1350\\\\\Rightarrow V_r=2965950.`

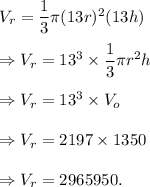
Thus, the volume of the resulting cone is 2965950 m³.