Hello there. To solve this question, we'll have to remember some properties about exponential growth function.
Given the exponential growth function modelling the number (in million) of Hispanic origin residents living in United States in 2000:
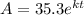
We have to determine the constant k, knowing that in 2010 the population has increased to 50.5 million.
In this case, since t is given in years after 2000, we know that t = 10 in 2010, hence plugging A = 50.5 and t = 10, we get:
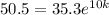
Divide both sides of the equation by a factor of 35.3

Notice in this case I didn't use an approximation to avoid future errors.
Take the natural logarithm on both sides, knowing that
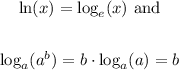
Hence we get
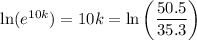
Divide both sides of the equation by a factor of 10
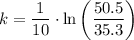
Using a calculator, we get the following approximation:
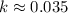
This is the value we're looking for.