Answer:
Books in shelf one are 33 and in shelf two are 22.
Explanation:
Let the two shelves contain x and y books.
So from first statement of the question
x + y = 55-------------(1)

y + 2x = 4y
3y = 2x ⇒
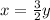 -------(2)
-------(2)
Now we put the value of x from equation 2 to equation 1
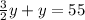
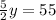
y = 22
Since x + y = 55 ⇒ 22 + x = 55
x = 33
So shelf one is having 33 books and shelf two is having 22 books.