Question

Please help me!
Calculus:

Answer 1

`\displaystyle f'(x) = ((x^2 + 2)(3x^4 - 6x^3 - 39x^2 - 36x + 14))/((x^2 - 3x - 2)^2)`

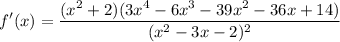
General Formulas and Concepts:

Pre-Algebra

Order of Operations: BPEMDAS

1. Brackets
2. Parenthesis
3. Exponents
4. Multiplication
5. Division
6. Addition
7. Subtraction

• Left to Right

Distributive Property

Algebra I

• Terms/Coefficients
• Expanding
• Factoring
• Functions
• Function Notation

Calculus

Derivatives

Derivative Notation

Derivative Property [Addition/Subtraction]:
`\displaystyle (d)/(dx)[f(x) + g(x)] = (d)/(dx)[f(x)] + (d)/(dx)[g(x)]`

Basic Power Rule:

• f(x) = cxⁿ
• f’(x) = c·nxⁿ⁻¹

Derivative Rule [Product Rule]:
`\displaystyle (d)/(dx) [f(x)g(x)]=f'(x)g(x) + g'(x)f(x)`

Derivative Rule [Quotient Rule]:
`\displaystyle (d)/(dx) [(f(x))/(g(x)) ]=(g(x)f'(x)-g'(x)f(x))/(g^2(x))`

Derivative Rule [Chain Rule]:
`\displaystyle (d)/(dx)[f(g(x))] =f'(g(x)) \cdot g'(x)`

Explanation:

*Note:

This is a pretty dense problem!

Step 1: Define

Identify

`\displaystyle f(x) = ((x + 3)(x^2 + 2)^2)/(x^2 - 3x - 2)`

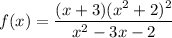
Step 2: Differentiate

1. Quotient Rule:
   `\displaystyle f'(x) = ((x^2 - 3x - 2)(d)/(dx)[(x + 3)(x^2 + 2)^2] - (d)/(dx)[(x^2 - 3x - 2)](x + 3)(x^2 + 2)^2)/((x^2 - 3x - 2)^2)`
2. Basic Power Rule [Derivative Property - Subtraction]:
   `\displaystyle f'(x) = ((x^2 - 3x - 2)(d)/(dx)[(x + 3)(x^2 + 2)^2] - (2x^(2 - 1) - 3x^(1 - 1) - 0)(x + 3)(x^2 + 2)^2)/((x^2 - 3x - 2)^2)`
3. Simplify:
   `\displaystyle f'(x) = ((x^2 - 3x - 2)(d)/(dx)[(x + 3)(x^2 + 2)^2] - (2x - 3)(x + 3)(x^2 + 2)^2)/((x^2 - 3x - 2)^2)`
4. Product Rule:
   `\displaystyle f'(x) = ((x^2 - 3x - 2) \bigg[ (d)/(dx)[(x + 3)](x^2 + 2)^2 + (x + 3)(d)/(dx)[(x^2 + 2)^2] \bigg] - (2x - 3)(x + 3)(x^2 + 2)^2)/((x^2 - 3x - 2)^2)`
5. [Brackets] Basic Power Rule [Derivative Property - Addition]:
   `\displaystyle f'(x) = ((x^2 - 3x - 2) \bigg[ (x^(1 - 1) + 0)(x^2 + 2)^2 + (x + 3)(d)/(dx)[(x^2 + 2)^2] \bigg] - (2x - 3)(x + 3)(x^2 + 2)^2)/((x^2 - 3x - 2)^2)`
6. [Brackets] Simplify:
   `\displaystyle f'(x) = ((x^2 - 3x - 2) \bigg[ (x^2 + 2)^2 + (x + 3)(d)/(dx)[(x^2 + 2)^2] \bigg] - (2x - 3)(x + 3)(x^2 + 2)^2)/((x^2 - 3x - 2)^2)`
7. [Brackets] Chain Rule:
   `\displaystyle f'(x) = ((x^2 - 3x - 2) \bigg[ (x^2 + 2)^2 + (x + 3)2(x^2 + 2)^(2 - 1) \cdot (d)/(dx)[(x^2 + 2)] \bigg] - (2x - 3)(x + 3)(x^2 + 2)^2)/((x^2 - 3x - 2)^2)`
8. [Brackets] Simplify:
   `\displaystyle f'(x) = ((x^2 - 3x - 2) \bigg[ (x^2 + 2)^2 + 2(x + 3)(x^2 + 2) \cdot (d)/(dx)[(x^2 + 2)] \bigg] - (2x - 3)(x + 3)(x^2 + 2)^2)/((x^2 - 3x - 2)^2)`
9. [Brackets] Basic Power Rule [Derivative Property - Addition]:
   `\displaystyle f'(x) = ((x^2 - 3x - 2) \bigg[ (x^2 + 2)^2 + 2(x + 3)(x^2 + 2) \cdot (2x^(2 - 1) + 0) \bigg] - (2x - 3)(x + 3)(x^2 + 2)^2)/((x^2 - 3x - 2)^2)`
10. [Brackets] Simplify:
    `\displaystyle f'(x) = ((x^2 - 3x - 2) \bigg[ (x^2 + 2)^2 + 2(x + 3)(x^2 + 2) \cdot 2x \bigg] - (2x - 3)(x + 3)(x^2 + 2)^2)/((x^2 - 3x - 2)^2)`
11. [Brackets] Multiply:
    `\displaystyle f'(x) = ((x^2 - 3x - 2) \bigg[ (x^2 + 2)^2 + 4x(x + 3)(x^2 + 2) \bigg] - (2x - 3)(x + 3)(x^2 + 2)^2)/((x^2 - 3x - 2)^2)`
12. [Brackets] Factor:
    `\displaystyle f'(x) = ((x^2 - 3x - 2) \bigg[ (x^2 + 2)[(x^2 + 2) + 4x(x + 3)] \bigg] - (2x - 3)(x + 3)(x^2 + 2)^2)/((x^2 - 3x - 2)^2)`
13. [Inner Brackets] (Parenthesis) Distribute 4x:
    `\displaystyle f'(x) = ((x^2 - 3x - 2) \bigg[ (x^2 + 2)[(x^2 + 2) + 4x^2 + 12x] \bigg] - (2x - 3)(x + 3)(x^2 + 2)^2)/((x^2 - 3x - 2)^2)`
14. [Inner Brackets] Combine like terms:
    `\displaystyle f'(x) = ((x^2 - 3x - 2)(x^2 + 2)(5x^2 + 12x + 2) - (2x - 3)(x + 3)(x^2 + 2)^2)/((x^2 - 3x - 2)^2)`
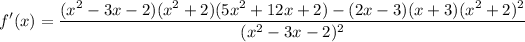
15. Factor:
    `\displaystyle f'(x) = ((x^2 + 2) \bigg[ (x^2 - 3x - 2)(5x^2 + 12x + 2) - (2x - 3)(x + 3)(x^2 + 2) \bigg])/((x^2 - 3x - 2)^2)`
16. [Brackets] Expand:
    `\displaystyle f'(x) = ((x^2 + 2) \bigg[ (5x^4 - 3x^3 - 44x^2 - 30x - 4) - (2x^4 + 3x^3 - 5x^2 + 6x - 18) \bigg])/((x^2 - 3x - 2)^2)`
17. [Brackets] Distribute negative:
    `\displaystyle f'(x) = ((x^2 + 2) \bigg[ 5x^4 - 3x^3 - 44x^2 - 30x - 4 - 2x^4 - 3x^3 + 5x^2 - 6x + 18 \bigg])/((x^2 - 3x - 2)^2)`
18. [Brackets] Combine like terms:
    `\displaystyle f'(x) = ((x^2 + 2)(3x^4 - 6x^3 - 39x^2 - 36x + 14))/((x^2 - 3x - 2)^2)`

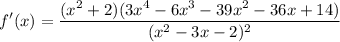
And we are done!

Topic: AP Calculus AB/BC (Calculus I/I + II)

Unit: Derivatives

Book: College Calculus 10e