Answer:
The given statement is false.
Explanation:
Given : For any function,
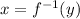 then
then
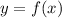
To find : The above statement is true or false?
Solution :
In the above statement the condition
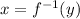 then
then
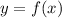 is valid for some function not for all.
is valid for some function not for all.
Which means the statement is not true.
Taking a contrary example,
A trigonometric function
The function
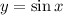 is one-one and onto in the domain
is one-one and onto in the domain
![[-(\pi)/(2),(\pi)/(2)]](https://img.qammunity.org/2018/formulas/mathematics/high-school/tkasi8yxua8qldm97wae00gihn3x1rec6x.png)
Thus, its inverse exists in
![[-(\pi)/(2),(\pi)/(2)]](https://img.qammunity.org/2018/formulas/mathematics/high-school/tkasi8yxua8qldm97wae00gihn3x1rec6x.png)
i.e.,
![\text{In }[-(\pi)/(2),(\pi)/(2)],\ y=\sin x \Rightarrow\ x=\sin^(-1)(y).](https://img.qammunity.org/2018/formulas/mathematics/high-school/2vcaw7h64ae1tiq1hutnj2yqejiofehci8.png)
It depends on the domain for the given statement to be true.
Therefore, The given statement is false.