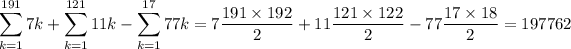Question

If we list all the natural numbers below 20 that are multiples of 7 or 11, we get 7, 11 and 14. The sum of these multiples is 32. What is the sum of all the multiples of 7 or 11 up to and including 1337?

Answer 1

Number of multiples of 7 up to 1337:
`\left\lfloor\frac{1337}7\right\rfloor=191`
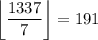
Number of multiples of 11 up to 1337:
`\left\lfloor(1337)/(11)\right\rfloor=121`
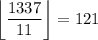
Number of multiples of 77 up to 1337:
`\left\lfloor(1337)/(77)\right\rfloor=17`

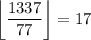
This means there are
`191+121-17=295` distinct multiples of 7 *or* 11 up to 1337.

The sum of these multiples is


`\displaystyle\sum_(k=1)^(191)7k+\sum_(k=1)^(121)11k-\sum_(k=1)^(17)77k`

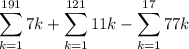
which can be computed using the well-known formula,


`\displaystyle\sum_(k=1)^nk=\frac{n(n+1)}2`

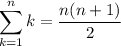
So you have


`\displaystyle\sum_(k=1)^(191)7k+\sum_(k=1)^(121)11k-\sum_(k=1)^(17)77k=7\frac{191*192}2+11\frac{121*122}2-77\frac{17*18}2=197762`