Question

Ten students begin college at the same time. The probability of graduating in four years is 63%. Which expanded expression shows the first and last terms of the expression used to find the probability that at least six will graduate in four years?

(106)×(0.63)6×(0.37)4+...+(1010)×(0.63)10×(0.37)∘=0.706

(105)×(0.63)5×(0.37)5+...+(1010)×(0.63)10×(0.37)∘=0.88

(100)×(0.63)∘×(0.37)10+...+(106)×(0.63)6×(0.37)4=0.540

(100)×(0.63)∘×(0.37)10+...+(105)×(0.63)5×(0.37)5=0.293

Answer 1

Answer: the answer is a!

Explanation:

Answer 2

Answer is option A

Explanation:

Let X be the number of students that graduate in four years. Let's suppose that the academic results of each student is indepent from other students. If we consider the event "To graduate in 4 years" as a success, we can model X as a binomial random variable. Then, the probability of having k students that graduate in 4 years is

`P(X = k ) \binom{10}{k}(0.63)^k(0.37)^(10-k)`

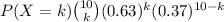
Since we want to know the probability that X is greater or equal to 6, we calculate the following

`P(X\geq 6)= P(X=6)+P(X=7)+... + P(X=10)`

`P(X\geq 6) = \binom{10}{6}(0.63)^6(0.37)^(4)+\dots + \binom{10}{10}(0.63)^(10)(0.37)^(0)`

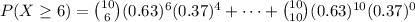
which is the option A