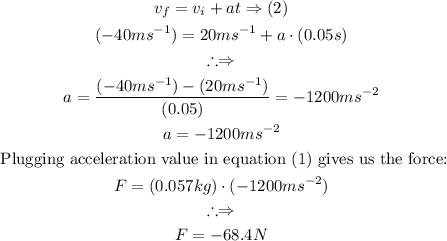Question

A tennis ball with a mass of 57 g and velocity of 20 m s' is struck by a racket. The ball's velocity changes to 40 m s' in the opposite direction. What is the average force acting on the ball if its time of contact with the racket is 50.0 ms?

Answer 1

`F=-68.4N`

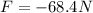
Step-by-step explanation: We need to calculate the average force needed to change the velocity of the ball from 20m/s ( forward ) to -40m/s ( Backwards ), the equations used are as follows:

`\begin{gathered} F=ma\Rightarrow(1) \\ v_f=v_i+at\Rightarrow(2)_{} \end{gathered}`

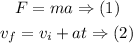
Here, in the (1) and (2) the unknows and knowns are as follows:

Plugging in the knowns in the (2) the acceleration is calculated as follows, and subsequently the force as well:

`\begin{gathered} v_f=v_i+at\Rightarrow(2)_{} \\ (-40ms^(-1))=20ms^(-1)+a\cdot(0.05s) \\ \therefore\Rightarrow \\ a=((-40ms^(-1))-(20ms^(-1)))/((0.05))=-1200ms^(-2) \\ a=-1200ms^(-2) \\ \text{ Plugging acceleration value in equation (1) gives us the force:} \\ F=(0.057kg)\cdot(-1200ms^(-2)) \\ \therefore\Rightarrow \\ F=-68.4N \\ \end{gathered}`