The given conic section is a hyperbola since this type of conic section can be represented by the equation:
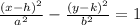
And the foci of a hyperbola with center at (h, k) are given by:
(h + c, k) and (h - c, k),
where
c = √(a² + b²)
So, for this hyperbola, we have:
h = -2
k = 3
a² = 16
b² = 9
Then, c is given by:
c = √(16+9) = √25 = 5
And the foci are:
(h + c, k) = (-2 + 5, 3) = (3, 3)
and
(h - c, k) = (-2 - 5, 3) = (-7, 3)
Thus, we can write the coordinates of both the foci as:
(-2 ± 5, 3)
Therefore, option C is correct.