Question

The following values represent exponential function ƒ(x) and linear function g(x). ƒ(1) = 2 g(1) = 2.5

ƒ(2) = 6 g(2) = 4
A. Determine whether or not there is a solution to the equation In 2-3 sentences describe whether there is a solution to the equation ƒ(x)=g(x) between x=1 and x=2. B. Use complete sentences to justify your claim

Answer 1

The function f(x) does not have a value of x that satisfies the given solutions, while the function g(x)=1.5+1. 

Answer 2

There does not exist any solution of
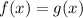`f(x)=g(x)` as thir graphs do not intersect.

Explanation:

We are given that,

The values of the exponential function f(x) are f(1)= 2 and f(2)= 6.

That is, we get,

`f(1)=2=2* 3^0`

`f(2)=2=2* 3^1`

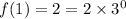
So, the function f(x) is
`f(x)=2(3)^x`.

Moreover, the values of the linear function g(x) are g(1) = 2.5 and g(2) = 4.

That is, the slope =
`(4-2.5)/(2-1)` = 1.5

Substituting the slope and point (1,2.5) in the linear equation
`y=mx+b`, where m is the slope, we get,

`2.5=1.5* 1+b`

i.e. b= 1

Thus, the function g(x) is
`g(x)=2.5x+1`.

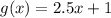Consider,
`f(x)=g(x)`

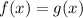
i.e.
`2(3)^x=2.5x+1`

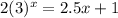
Now, the function f(x) is exponentially increasing and the linear function g(x) is increasing between x= 1 and x= 2, but there is no point where the graphs of the functions are intersecting.

Thus, there is no solution of the equation
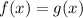`f(x)=g(x)`.