Final answer:
The best prediction of the snake population in the year 2014 is approximately 5190.
Step-by-step explanation:
To predict the snake population in the year 2014, we need to use the given rate of decline. The population is decreasing at a rate of 2.7% per year. We can calculate the population in 2014 by using the formula:
Population in 2014 = Population in 2009 × (1 - Rate of decline)(Year difference)
Year difference = 2014 - 2009 = 5 years
Population in 2014 ≈ 6000 ×
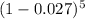 ≈ 6000 × 0.865 ≈ 5190
≈ 6000 × 0.865 ≈ 5190
Therefore, the best prediction of the snake population in the year 2014 is approximately 5190.