In △FGH, h = 10, m∠F = 65°, and m∠G = 35°. What is the length of g? Use the law of sines to find the answer. 5.8 units 6.7 units 9.2 units 9.8 units

Question

asked Mar 16, 2018 65.5k views

2 Answers

Igor Adamenko · Answer 1 · 2018-03-20T11:09:48+0000

Answer:

Option A is correct.

The length of g = 5.8 units.

Explanation:

In triangle FGH

Given:
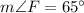$m\angle F = 65^(\circ)$ and
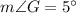
$m\angle G = #5^(\circ)$

As we know,

The sum of measures of the three angles of any triangle is 180 degree.

In triangle FGH

$m\angle F+m\angle G+ m\angle H=180^(\circ)$

Substitute the given values of angle F and angle G we get

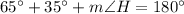
$65^(\circ)+35^(\circ)+ m\angle H=180^(\circ)$

or

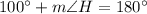
$100^(\circ)+ m \angle H = 180^(\circ)$

Simplify:

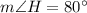
$m\angle H = 80^(\circ)$

To find the length of g;

Use sine law: Sine rule is an equation relating the lengths of the sides of a triangle to the sines of its angles.

In ΔFGH as shown below in figure

By sine law we have;

$(\sin H)/(h) = (\sin G)/(g)$

Now, substitute the values angle H = 80°, angle G = 35° and h =10 units we have;

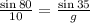
$(\sin 80)/(10) = (\sin 35)/(g)$

or

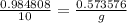
(0.984808)/(10)=(0.573576)/(g)

we can write this as;

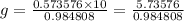
g = (0.573576 * 10)/(0.984808) =(5.73576)/(0.984808)

Simplify:

g = 5.82424188 ≈ 5.8 units.

Therefore, the length of g is, 5.8 units