Now, Now,We are given the following vectors:
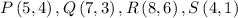
We are asked to determine the following vector:
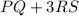
First, we will determine the vector PQ and RS. To determine PQ we use the following:
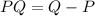
This means we need to subtract "P" from "Q". We do that by subtracting each component of the points, like this:
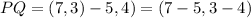
Solving the operations:
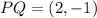
Now, we use a similar procedure to determine RS:
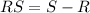
Substituting we get:
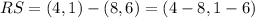
Solving the operations:
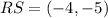
Now, we substitute the values in the vector we are looking for:
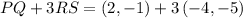
Now, we solve the product by multiplying both components of RS:
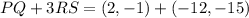
Now, we solve the addition by adding each corresponding component:
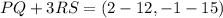
Solving the operations:
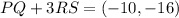
And thus we have determined the components.
Part B. We area asked to determine the magnitude of the vector. To do that we will use the following:
Given a vector of the form:
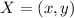
Its magnitude is:
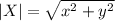
This means that the magnitude is the square root of the sum of the square of the components. Applying the formula we get:
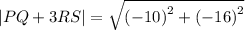
Now, we solve the squares:
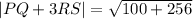
Solving the addition:
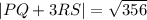
Now, we factor the term inside the radical as follows:
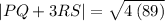
Now, we distribute the radical:
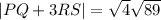
Taking the left square root:
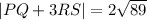
And thus we have determined the magnitude.