Question

Raj writes a polynomial expression in standard form using one variable, a, that has 4 terms and is degree 5. Nicole writes a polynomial expression in standard form using one variable, a, that has 3 terms and is degree 2. Raj and Nicole’s polynomial expressions are added to create a sum, written in standard form. What can you determine about the number of terms of the sum? The maximum number of terms of the sum is ___ but could be less.

Answer 1

The sum's degree will be equal to the highest degree of the two polynomials. Out of the two polynomials being added, the higher degree is 5. The sum will be degree 5.

Answer 2

6 Terms

Explanation:

Raj's polynomial in variable, a, has 4 terms and is of degree 5.

Let the polynomial be:
`Aa^5+Ba^4+Ca^3+Da^2`

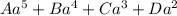
Nicole's polynomial in variable, a, has 3 terms and is of degree 2.

Let the polynomial be:
`Ea^2+Fa+G`

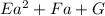
When you sum the two polynomials:

`Aa^5+Ba^4+Ca^3+Da^2+Ea^2+Fa+G\\Aa^5+Ba^4+Ca^3+(D+E)a^2+Fa+G`

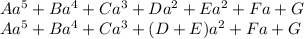
The new polynomial will have a degree of 5 and the maximum number of terms of the sum is 6 but could be less.