Question

While sailing a boat offshore, Bobby sees a lighthouse and calculates thatthe angle of elevation to the top of the lighthouse is 3°. When she sails her boat700 m closer to the lighthouse, she finds that the angle of elevation is now 5°.How tall, to the nearest tenth of a meter, is the lighthouse?

Answer 1

Given

While sailing a boat offshore, Bobby sees a lighthouse and calculates that

the angle of elevation to the top of the lighthouse is 3°.

When she sails her boat 700 m closer to the lighthouse, she finds that the angle of elevation is now 5°.

To find:

How tall, to the nearest tenth of a meter, is the lighthouse?

Step-by-step explanation:

It is given that,

While sailing a boat offshore, Bobby sees a lighthouse and calculates that

the angle of elevation to the top of the lighthouse is 3°.

When she sails her boat 700 m closer to the lighthouse, she finds that the angle of elevation is now 5°.

That implies,

`\tan3\degree=(y)/(x+700)`

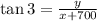
Also,

`\begin{gathered} \tan5\degree=(y)/(x) \\ y=x\tan5\degree \end{gathered}`

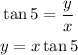
Therefore,

`\begin{gathered} \tan3\degree=(x\tan5\degree)/(x+700) \\ (x+700)\tan3\degree=x\tan5\degree \\ x\tan3\degree+700\tan3\degree=x\tan5\degree \\ (\tan5\degree-\tan3\degree)x=700\tan3\degree \\ 0.0351x=36.6854 \\ x=1045.7m \end{gathered}`

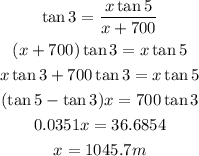
Then,

`\begin{gathered} \tan5\degree=(y)/(1045.7) \\ y=1045.7\tan5\degree \\ y=91.5m \end{gathered}`

Hence, the height of the light house is, 91.5m.