Given
While sailing a boat offshore, Bobby sees a lighthouse and calculates that
the angle of elevation to the top of the lighthouse is 3°.
When she sails her boat 700 m closer to the lighthouse, she finds that the angle of elevation is now 5°.
To find:
How tall, to the nearest tenth of a meter, is the lighthouse?
Step-by-step explanation:
It is given that,
While sailing a boat offshore, Bobby sees a lighthouse and calculates that
the angle of elevation to the top of the lighthouse is 3°.
When she sails her boat 700 m closer to the lighthouse, she finds that the angle of elevation is now 5°.
That implies,
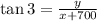
Also,
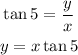
Therefore,
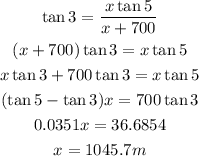
Then,
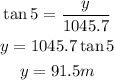
Hence, the height of the light house is, 91.5m.