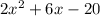Answer:
A simplified polynomial expression in standard form to represent the area of the rectangle below is:
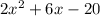
Explanation:
We are given a rectangular figure such that the length of one side is given as: 2x-4
while the other side is labelled as: x+4.
Let us assume that the length of rectangle(l)= 2x-4
and width or breadth of rectangle(b)=x+5
We know that the area of rectangle(A) is given as:
A=l×b.
A=(2x-4)×(x+5)
A=2x(x+5)-4(x+5)
A=2x^2+10x-4x-20
A=2x^2+6x-20.
Hence, the polynomial expression for the area of rectangle is a polynomial of degree 2 and is given by: