Question

Evaluate each function at the given value using synthetic substitution

Answer 1

By the polynomial remainder theorem, the remainder upon dividing a polynomial
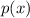
`p(x)` by a linear factor
`x-c` is equal to the value of
`p(c)`.

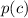
So what you need to do is use synthetic division to compute the quotient and remainder of


`(f(m))/(m+4)=(-3m^4-17m^3-24m^2-11m+11)/(m+4)`

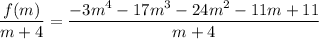
Synthetic division yields

-4 ... | ... -3 ... -17 ... -24 ... -11 ... 11
... ... | ... ... 12 ... 20 ... 16 ...-20
------------------------------------------------
... ... | ... -3 ..... -5 ..... -4 ...... 5 .... -9

which translates to a quotient of
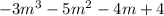
`-3m^3-5m^2-4m+4` and a remainder term of
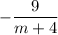
`-(9)/(m+4)`. So
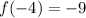
`f(-4)=-9`.