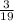Question

A bag contains 10 blue, 6 green, and 4 red marbles. You choose one marble. Without putting it back, you choose a second marble. What is the probability that you first choose a green marble and then a blue marble?

Answer 1

P(green then blue) = 3/19

Explanation:

Answer 2

`(3)/(19)`

Explanation:

Given :

A bag contains 10 blue, 6 green, and 4 red marbles.

You choose one marble. Without putting it back, you choose a second marble.

To Find: What is the probability that you first choose a green marble and then a blue marble?

Solution:

No. of blue balls = 10

No. of green balls =6

No. of red marbles =4

Total no. of marbles = 10+6+4 =20

Since we are given that first he choose a green marble

So, probability of getting green marble :

`\frac{\text{No. of green marbles}}{\text{total no. of marbles}}`

=
`(6)/(20)`

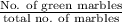
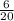
Since he choose second marble without replacement

So, after choosing first ball . The total no. of balls will be 19

So, Probability of getting blue marble in second draw :

`\frac{\text{No. of blue marbles}}{\text{total no. of marbles}}`

=
`(10)/(19)`

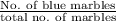
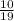
The probability that you first choose a green marble and then a blue marble:

`=(6)/(20)*(10)/(19)`

`=(3)/(19)`

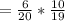
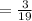
Hence the probability that you first choose a green marble and then a blue marble is
`(3)/(19)`