Question

A 2000 gallon fish aquarium can be filled by water flowing at a constant rate in 10 hours. When a decorativve rock is placed in the aquarium, it can be filled in 9.5 hours. Find the volume of the rock in cubic feet

Answer 1

The volume of the rock is 13.368 cubic feet.

Explanation:

The volume of the rock (
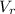`V_(r)`), measured in gallons, is equal to the volume of the fish aquarium without the decorative rock (
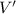`V'`) minus the volume of the fish aquarium with the decorative rock (
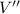`V''`), both measured in gallons.

Since the water flow is at constant rate, the volume of the rock is expressed by the following equation:

`V_(r) = V' - V''`

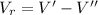
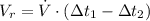`V_(r) = \dot V \cdot (\Delta t_(1)-\Delta t_(2))` (1)

Where:

`\dot V` - Flow rate, measured in gallons per hour.

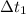`\Delta t_(1)` - Filling time of the fish aquarium without the decorative rock, measured in hours.

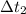`\Delta t_(2)` - Filling time of the fish aquarium with the decorative rock, measured in hours.

And the flow rate is:

`\dot V = (2000\,gal)/(10\,h)`

`\dot V = 200\,(gal)/(h)`

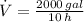
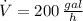
The flow rate is 200 gallons per hour.

If we know that
`\dot V = 200\,(gal)/(h)`,
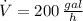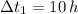`\Delta t_(1) = 10\,h` and
`\Delta t_(2) = 9.5\,h`, then the volume of the rock is:

`V_(r) = \left(200\,(gal)/(h)\right)\cdot (10\,h-9.5\,h)`

`V_(r) = 100\,gal`

`V_(r) = 13.368\,ft^(3)`

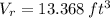
The volume of the rock is 13.368 cubic feet.