Part A. We are asked to determine the force exerted on a charge placed on point Z. To do that we will use the fact that charges with the same sign will attract each other and charges with a different sign will repel each other. Therefore, we can construct the following free body diagram:
Since q3 and q2 are both negative they repel each other and since q1 is positive this means that q3 and q1 will attract each other.
To determine the magnitude of the forces we will use Coulomb's law:
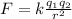
Where:

For the force between q1 and q3 we have:
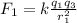
For the force between q3 and q2 we have:

Now, the net force is the difference between F2 and F1 since the force act in different directions, therefore, we have:
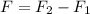
we have taken the left direction to be negative and the right direction to be positive. Now, we substitute Coulomb's law:
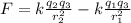
We can take "kq3" as a common factor:

The distance from q1 to q3 is:
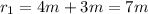
The distance from q2 and q3 is:
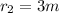
Now, we substitute the values:
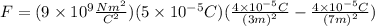
Solving the operations:
Solving the operations:
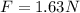
Therefore, the net force is 1.63 Newtons to the right.
Part B. To calculate the electric potential energy we will use the following formula:
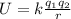
To determine the total energy we add the energy for both pairs of charges, like this:
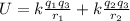
We can take "kq3" as a common factor:
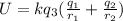
Now, we substitute the values:
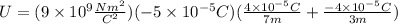
Solving the operations we get
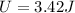
Therefore, the energy is 3.42 Joules.