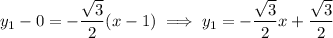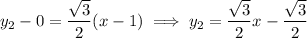You're looking for
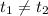
such that
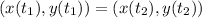
.
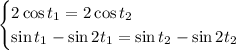
Recall that
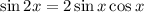
, so the second equation can be written as
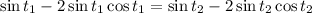
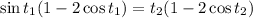
Since
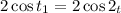
, and assuming
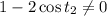
, you get
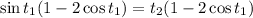
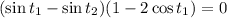
which admits two possibilities; either
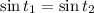
or
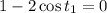
. In the first case, since we're assuming
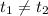
, we can use the fact that
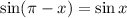
to arrive at a solution of
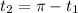
.
In the second case, you have
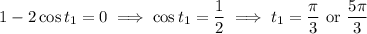
Let's check which of these solutions work. If
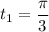
, then the sine equation suggests
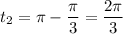
. However,
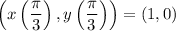
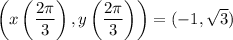
so in fact this is an extraneous solution. So let's return to the first equation in the system,
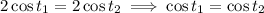
Again, assuming
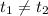
, we can use the fact that
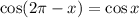
to arrive at a solution of
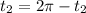
. Now, if
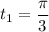
, we get
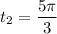
. Let's check if this works:
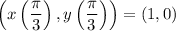
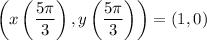
Indeed, this solution works! So the curve intersects itself at the point (1,0), which the curve passes for the first time through when
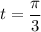
and the second time when
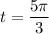
.
Now, to find the tangent line, we need to compute the derivative of
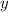
with respect to

. You have
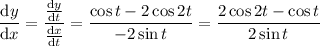
When
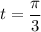
, you have a slope of
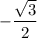
; at
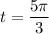
, the slope is
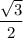
.
The tangent lines are then