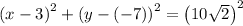Question

How is the equation of this circle written in standard form?

x2 + y2 - 6x + 14y = 142

Answer 1

( x - 3 )^2 + ( y + 7 )^2 = 200

Answer 2

The equation of circle becomes
`\left(x-3\right)^2+\left(y-\left(-7\right)\right)^2=\left(10√(2)\right)^2`

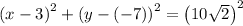
Explanation:

Given equation of circle
`x^2+y^2-6x+14y=142`

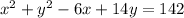
We have to write the equation of this circle written in standard form.

The standard equation of a circle with (h,k) as center and radius r, is given by

`(x-h)^2+(y-k)^2=r^2\\`

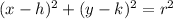
For the given equation of circle
`x^2+y^2-6x+14y=142`

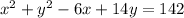
making perfect squares ,

Rearranging terms, we have,

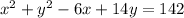`x^2+y^2-6x+14y=142` as
`x^2-6x+y^2+14y=142`

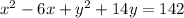
Applying
`(a+b)^2=a^2+b^2+2ab\\ (a-b)^2=a^2+b^2-2ab`

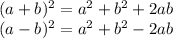
We have
`x^2-6x+y^2+14y=142`

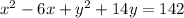
To make
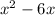`x^2-6x` a perfect square add and subtract 3²= 9 , we get,

`x^2-6x+9-9+y^2+14y=142`

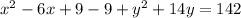
Similarly, To make
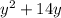`y^2+14y` a perfect square add and subtract 7²= 49 we get,

`x^2-6x+9-9+y^2+14y+49-49=142`

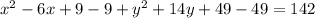
Simplify, we get,

`(x-3)^2+(y+7)^2=142+49+9`

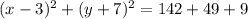
Simplify , we have,

`(x-3)^2+(y+7)^2=200`

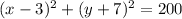
Thus, the equation of circle becomes
`\left(x-3\right)^2+\left(y-\left(-7\right)\right)^2=\left(10√(2)\right)^2`