Question

A polynomial equation with rational coefficients has the roots 3+ square root 6, 2- square root 5. Find the two additional roots

Answer 1

the other 2 roots will be the conjugates of the above.
In other words they are
3 - sqrt6 and 2 + sqrt5

Answer 2

`(3-√(6)) and (2+√(5))`

Explanation:

If a polynomial equation with rational coefficients is
`ax^2+bx+c=0`, then by quadratic formula

`x=(b\pm√(b^2-4ac))/(2a)`

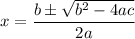
where, a,b and c are rational number.

If
`√(b^2-4ac)` is an irrational number, then we have ± sign before the irrational number.

It is given that
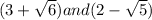`(3+√(6)) and (2-√(5))` are two roots of a polynomial equation with rational coefficients. Here,
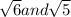`√(6) and √(5)` are irrational numbers.

So, the root of the polynomial equation are

`(3\pm √(6)) and (2\pm √(5))`

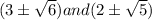
Therefore, the remaining roots of the polynomial equation are
`(3-√(6)) and (2+√(5))`.